Welcome to RSTSR

Welcome to RSTSR, a rust tensor toolkit library.

RSTSR is still in early development, and has not been published to crates.io. Current document does not bound to any version of RSTSR.

To start with, you may try to run the following code:

#![allow(unused)]
fn main() {
use rstsr_core::prelude::*;

#[test]
fn welcome() {
    // 3x2 matrix with c-contiguous memory layout
    let a = rt::asarray((vec![6., 2., 7., 4., 8., 5.], [3, 2].c()));

    // 2x4x3 matrix by arange and reshaping
    let b = rt::arange(24.).into_shape([2, 4, 3]);

    // broadcasted matrix multiplication
    let c = b % a;

    // print layout of the result
    println!("{:?}", c.layout());
    // output:
    // 3-Dim, contiguous: Cc
    // shape: [2, 4, 2], stride: [8, 2, 1], offset: 0

    // print the result
    println!("{:6.1}", c)
    // output:
    // [[[   23.0   14.0]
    //   [   86.0   47.0]
    //   [  149.0   80.0]
    //   [  212.0  113.0]]
    //
    //  [[  275.0  146.0]
    //   [  338.0  179.0]
    //   [  401.0  212.0]
    //   [  464.0  245.0]]]
}
}

Tensor creation

In many cases, we import RSTSR by following code:

#![allow(unused)]
fn main() {
use rstsr_core::prelude::*;
}

It may be possible that names of RSTSR structs or functions clash with other crates. You may wish to import RSTSR by following code if that happens:

#![allow(unused)]
fn main() {
use rstsr_core::prelude::rstsr as rt;
use rt::rstsr_traits::*;
}

1. Converting Rust Vector to RSTSR Tensor

1.1 1-D tensor from rust vector

RSTSR tensor can be created by (owned) vector object.

In the following case, memory of vector object vec will be transferred to tensor object tensor¹. Except for relatively small overhead (generating layout of tensor), no explicit data copy occurs.

#![allow(unused)]
fn main() {
    // move ownership of vec to 1-D tensor (default CPU device)
    let vec = vec![1.0, 2.968, 3.789, 4.35, 5.575];
    let tensor = rt::asarray(vec);

    // only print 2 decimal places
    println!("{:.2}", tensor);
    // output: [ 1.00 2.97 3.79 4.35 5.58]
}

#![allow(unused)]
fn main() {
    // move ownership of vec to 1-D tensor
    // custom CPU device that limits threads to 4
    let vec = vec![1, 2, 3, 4, 5];
    let device = DeviceFaer::new(4);
    let tensor = rt::asarray((vec, &device));
    println!("{:?}", tensor);

    // output:
    // === Debug Tensor Print ===
    // [ 1 2 3 4 5]
    // DeviceFaer { base: DeviceCpuRayon { num_threads: 4 } }
    // 1-Dim, contiguous: CcFf
    // shape: [5], stride: [1], offset: 0
    // Type: rstsr_core::tensorbase::TensorBase<rstsr_core::tensor::data::DataOwned<rstsr_core::storage::device::Storage<i32, rstsr_core::device_faer::device::DeviceFaer>>, [usize; 1]>
}

1.2 $n$-D tensor from rust vector

For $n$-D tensor, the recommended way to build from existing vector, without explicit memory copy, is

• first, build 1-D tensor from contiguous memory;
• second, reshape to the $n$-D tensor you desire;

#![allow(unused)]
fn main() {
    // generate 2-D tensor from 1-D vec, without explicit data copy
    let vec = vec![1, 2, 3, 4, 5, 6];
    let tensor = rt::asarray(vec).into_shape_assume_contig([2, 3]);
    println!("{:}", tensor);

    // if you feel function `into_shape_assume_contig` ugly, following code also works
    let vec = vec![1, 2, 3, 4, 5, 6];
    let tensor = rt::asarray(vec).into_shape([2, 3]);
    println!("{:}", tensor);

    // and even more concise
    let vec = vec![1, 2, 3, 4, 5, 6];
    let tensor = rt::asarray((vec, [2, 3]));
    println!("{:}", tensor);

    // output:
    // [[ 1 2 3]
    //  [ 4 5 6]]
}

We do not recommend generating $n$-D tensor from nested vectors, i.e. Vec<Vec<T>>. Explicit memory copy will always occur anyway in this case. So for nested vectors, you may wish to first generate a flattened Vec<T>, then perform reshape on this:

#![allow(unused)]
fn main() {
    let vec = vec![vec![1, 2, 3], vec![4, 5, 6]];

    // generate 2-D tensor from nested Vec<T>, WITH EXPLICIT DATA COPY
    // so this is not recommended for large data
    let (nrow, ncol) = (vec.len(), vec[0].len());
    let vec = vec.into_iter().flatten().collect::<Vec<_>>();

    // please also note that nested vec is always row-major, so using `.c()` is more appropriate
    let tensor = rt::asarray((vec, [nrow, ncol].c()));
    println!("{:}", tensor);
    // output:
    // [[ 1 2 3]
    //  [ 4 5 6]]
}

2. Converting Rust Slices to RSTSR TensorView

Rust language is extremely sensitive to ownership of variables, unlike python. For rust, reference of contiguous memory of data is usually represented as slice &[T]. For RSTSR, this is stored by TensorView².

#![allow(unused)]
fn main() {
    // generate 1-D tensor view from &[T], without data copy
    let vec = vec![1, 2, 3, 4, 5, 6];
    let tensor = rt::asarray(&vec);

    // note `tensor` is TensorView instead of Tensor, so it doesn't own data
    println!("{:?}", tensor);

    // check if pointer of vec and tensor's storage are the same
    assert_eq!(vec.as_ptr(), tensor.storage().rawvec().as_ptr());

    // output:
    // === Debug Tensor Print ===
    // [ 1 2 3 4 5 6]
    // DeviceFaer { base: DeviceCpuRayon { num_threads: 0 } }
    // 1-Dim, contiguous: CcFf
    // shape: [6], stride: [1], offset: 0
    // Type: rstsr_core::tensorbase::TensorBase<rstsr_core::tensor::data::DataRef<rstsr_core::storage::device::Storage<i32, rstsr_core::device_faer::device::DeviceFaer>>, [usize; 1]>
}

You may also convert mutable slice &mut [T] into tensor. For RSTSR, this is stored by TensorMut:

#![allow(unused)]
fn main() {
    // generate 2-D tensor mutable view from &mut [T], without data copy
    let mut vec = vec![1, 2, 3, 4, 5, 6];
    let mut tensor = rt::asarray((&mut vec, [2, 3]));

    // you may perform arithmetic operations on `tensor`
    tensor *= 2;
    println!("{:}", tensor);
    // output:
    // [[ 2 4 6]
    //  [ 8 10 12]]

    // you may also see variable `vec` is also changed
    println!("{:?}", vec);
    // output: [2, 4, 6, 8, 10, 12]
}

3. Intrinsic RSTSR Tensor Creation Functions

3.1 1-D tensor creation functions

Most useful 1-D tensor creation functions are arange and linspace.

arange creates tensors with regularly incrementing values. Following code shows multiple ways to generate tensor³.

#![allow(unused)]
fn main() {
    let tensor = rt::arange(10);
    println!("{:}", tensor);
    // output: [ 0 1 2 ... 7 8 9]

    let device = DeviceFaer::new(4);
    let tensor = rt::arange((2.0, 10.0, &device));
    println!("{:}", tensor);
    // output: [ 2 3 4 5 6 7 8 9]

    let tensor = rt::arange((2.0, 3.0, 0.1));
    println!("{:}", tensor);
    // output: [ 2 2.1 2.2 ... 2.7000000000000006 2.8000000000000007 2.900000000000001]
}

linspace will create tensors with a specified number of elements, and spaced equally between the specified beginning and end values.

#![allow(unused)]
fn main() {
    use num::complex::c64;

    let tensor = rt::linspace((0.0, 10.0, 11));
    println!("{:}", tensor);
    // output: [ 0 1 2 ... 8 9 10]

    let tensor = rt::linspace((c64(1.0, 2.0), c64(-15.0, 10.0), 5, &DeviceFaer::new(4)));
    println!("{:}", tensor);
    // output: [ 1+2i -3+4i -7+6i -11+8i -15+10i]
}

3.2 2-D tensor creation functions

Most useful 2-D tensor creation functions are eye and diag.

eye generates identity matrix. In many cases, you may just provide the number of rows, and eye(n_row) will return a square identity matrix, or eye((n_row, &device)) if device is of concern. If you may wish to generate a rectangular identity matrix with offset, you may call eye((n_row, n_col, offset)).

#![allow(unused)]
fn main() {
    let device = DeviceFaer::new(4);
    let tensor: Tensor<f64, _> = rt::eye((3, &device));
    println!("{:}", tensor);
    // output:
    // [[ 1 0 0]
    //  [ 0 1 0]
    //  [ 0 0 1]]

    let tensor: Tensor<f64, _> = rt::eye((3, 4, -1));
    println!("{:}", tensor);
    // output:
    // [[ 0 0 0 0]
    //  [ 1 0 0 0]
    //  [ 0 1 0 0]]
}

diag generates diagonal 2-D tensor from 1-D tensor, or generate 1-D tensor from diagonal of 2-D tensor. diag is defined as overloaded function; if offset of diagonal is of concern, you may wish to call diag((&tensor, offset)).

#![allow(unused)]
fn main() {
    let vec = rt::arange(3) + 1;
    let tensor = vec.diag();
    println!("{:}", tensor);
    // output:
    // [[ 1 0 0]
    //  [ 0 2 0]
    //  [ 0 0 3]]

    let tensor = rt::arange(9).into_shape([3, 3]);
    let diag = tensor.diag();
    println!("{:}", diag);
    // output: [ 0 4 8]
}

3.3 General $n$-D tensor creation functions

Most useful $n$-D tensor creation functions are zeros, ones, empty. These functions can build tensors with any desired shape (or layout).

• zeros fill tensor with all zero values;
• ones fill tensor with all one values;
• unsafe empty give tensor with uninitialized values;
• fill fill tensor with the same value provided by user;

We will mostly use zeros as example. For common usages, you may wish to generate a tensor with shape (or additionally device bounded to tensor):

#![allow(unused)]
fn main() {
    // generate tensor with default device
    let tensor: Tensor<f64, _> = rt::zeros([2, 2, 3]); // Tensor<f64, Ix3>
    println!("{:}", tensor);
    // output:
    // [[[ 0 0 0]
    //   [ 0 0 0]]
    //
    //  [[ 0 0 0]
    //   [ 0 0 0]]]

    // generate tensor with custom device
    // note: the third type annotation refers to device type, hence is required if not default device
    // Tensor<f64, Ix2, DeviceCpuSerial>
    let tensor: Tensor<f64, _, _> = rt::zeros(([3, 4], &DeviceCpuSerial));
    println!("{:}", tensor);
    // output:
    // [[ 0 0 0 0]
    //  [ 0 0 0 0]
    //  [ 0 0 0 0]]
}

You may also specify layout: whether it is c-contiguous (row-major) or f-contiguous (column-major)⁴. In RSTSR, attribute function c and f are used for generating c/f-contiguous layouts:

#![allow(unused)]
fn main() {
    // generate tensor with c-contiguous
    let tensor: Tensor<f64, _> = rt::zeros([2, 2, 3].c());
    println!("shape: {:?}, stride: {:?}", tensor.shape(), tensor.stride());
    // output: shape: [2, 2, 3], stride: [6, 3, 1]

    // generate tensor with f-contiguous
    let tensor: Tensor<f64, _> = rt::zeros([2, 2, 3].f());
    println!("shape: {:?}, stride: {:?}", tensor.shape(), tensor.stride());
    // output: shape: [2, 2, 3], stride: [1, 2, 4]
}

A special $n$-D case is 0-D tensor (scalar). You may also generate 0-D tensor by zeros:

#![allow(unused)]
fn main() {
    // generate 0-D tensor
    let mut a: Tensor<f64, _> = rt::zeros([]);
    println!("{:}", a);
    // output: 0

    // 0-D tensor arithmetics are also valid
    a += 2.0;
    println!("{:}", a);
    // output: 2

    let b = rt::arange(3.0) + 1.0;
    let c = a + b;
    println!("{:}", c);
    // output: [ 3 4 5]
}

You may also initialize a tensor without filling specific values. This is unsafe.

#![allow(unused)]
fn main() {
    // generate empty tensor with default device
    let tensor: Tensor<i32, _> = unsafe { rt::empty([10, 10]) };
    println!("{:?}", tensor);
}

This crate has not implemented API for random initialization. However, you may still able to perform this kind of task by asarray.

#![allow(unused)]
fn main() {
    use rand::rngs::StdRng;
    use rand::{Rng, SeedableRng};

    // generate f-contiguous layout and it's memory buffer size
    let layout = [2, 3].f();
    let size = layout.size();

    // generate random numbers to vector
    let seed: u64 = 42;
    let mut rng = StdRng::seed_from_u64(seed);
    let random_vec: Vec<f64> = (0..size).map(|_| rng.gen()).collect();

    // create a tensor from random vector and f-contiguous layout
    let tensor = rt::asarray((random_vec, layout));

    // print tensor with 3 decimal places with width of 7
    println!("{:7.3}", tensor);
}

Tensor Structure and Ownership

In rust, strict rules are applied to ownership and lifetime (related to concept of view). It is important to know how data (memory of large bulk of floats) is stored and handled, and whether a variable owns or references these data.

As a tensor crate, we also hope to have some unified API functions or operations, that can handle computations both on owned and referenced tensors. In vulgar words, numpy is convenient, and one may hope to code pythonicly in rust.

In this section, we will try to show how RSTSR constructs tensor struct and different ownerships of tensors works.

1. Tensor Structure

RSTSR tensor learns a lot from rust crate ndarray. Structure and usage of RSTSR's TensorBase is similar to ndarray's ArrayBase; however, they are different in some key points.

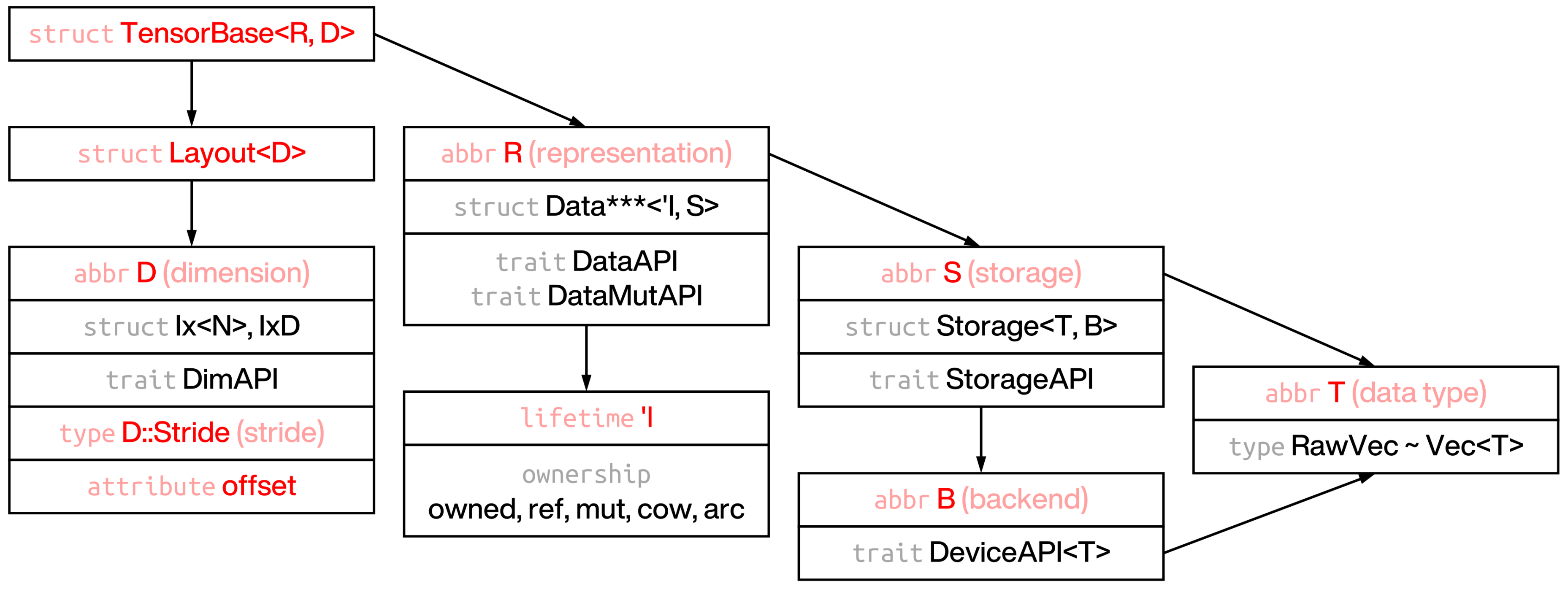
• Tensor is composed by data (how data is stored in memory bulk) and layout (how tensor is represented).
• Layout is composed by shape (shape of tensor), stride (how each value is accessed from memory bulk), and offset (where the tensor starts)¹.
• Data is combination of the actual memory storage with the lifetime annotation to it. Currently, 5 ownership types are supported. The first two (owned and referenced) are the most important².
  • Owned (Tensor<T, D, B>)
  • Referenced (TensorView<'l, T, D, B> or TensorRef<'l, T, D, B>)
  • Mutablly referenced (TensorViewMut<'l, T, D, B> or TensorMut<'l, T, D, B>)
  • Clone on write (not mutable enum of owned and referenced, TensorCow<'l, T, D, B>)
  • Atomic reference counted (safe in threading, TensorArc<T, D, B>)
• Storage is composed by raw memory (type RawVec) and backend (device)³
• The actual memory bulk will be stored as Vec<T> in CPU, and this can be configured by trait type RawVec⁴.

2. Ownership Conversion

2.1 Tensor to tensor ownership conversion

Different ownerships can be converted to each other. However, some conversion functions may have some costs (explicit memory copy).

• view gives TensorView<'l, T, D, B>.
  • This function will always not perform memory copy (of tensor data) in any cases. For this part, it is virtually zero-cost.
  • It will still perform clone of tensor layout, so still some overhead occurs. For large tensor, it is cheap.
• view_mut gives TensorMut<'l, T, D, B>.
  • In rust, either many const references or only one mutable reference is allowed. This is also true for TensorView as const reference and TensorMut as mutable reference.
• into_owned_keep_layout gives Tensor<T, D, B>.
  • For Tensor, this is free of memory copy;
  • For TensorView and TensorMut, this requires explicit memory copy. Note that it is usually more proper to use into_owned in this case.
  • For TensorArc, this is free of memory copy, but please note that it may panic when strong reference count is not exactly one. You may use tensor.data().strong_count() to check strong reference count.
  • For TensorCow, if it is owned (DataCow::Owned), then it is free of memory copy; if it is reference (DataCow::Ref), then it requires explicit memory copy.
• into_owned also gives Tensor<T, D, B>.
  • This function is different to into_owned_keep_layout, in that into_owned only not copy memory when layout of tensor covers all memory (size of memory bulk is the same to size of tensor layout). Calling into_owned to any non-trivial slicing of tensor will incur memory copy.
  • Also note that, if you just want to shrink the memory to a slice of tensor, using into_owned is more appropriate.
  • For TensorView and TensorMut, using into_owned will copy less memory into_owned_keep_layout. So into_owned is preferrable for tensor views.
• into_cow gives TensorCow<'l, T, D, B>.
  • This function does not have any cost.
• into_shared_keep_layout and into_shared gives TensorArc<'l, T, D, B>. This is similar to into_owned_keep_layout and into_owned.

An example for tensor ownership conversion follows:

#![allow(unused)]
fn main() {
    // generate 1-D owned tensor
    let tensor = rt::arange(12);
    let ptr_1 = tensor.rawvec().as_ptr();

    // this will give owned tensor with 2-D shape
    // since previous tensor is contiguous, this will not copy memory
    let mut tensor = tensor.into_shape([3, 4]);
    tensor += 1; // inplace operation
    let ptr_2 = tensor.rawvec().as_ptr();

    // until now, memory has not been copied
    assert_eq!(ptr_1, ptr_2);

    // convert to view
    let tensor_view = tensor.view();

    // from view to owned tensor
    let tensor = tensor_view.into_owned();
    let ptr_3 = tensor.rawvec().as_ptr();

    // now memory has been copied
    assert_ne!(ptr_2, ptr_3);
}

2.2 Tensor and Vec<T> conversion

We have already touched some array creation functions in previous section. Here we will cover more on this topic.

Converting between Tensor and Vec<T> or &[T] can be useful if

• transfer data to other objects (such as candle, ndarray, nalgebra),
• need pointer to perform FFI operations (such as BLAS, Lapack),
• export data to be further serialized.

There are some useful functions to perform Tensor to Vec<T>:

• to_vec(): copy 1-D tensor to vector, requires memory copy;
• into_vec(): move 1-D tensor to vector if memory is contiguous; otherwise copy 1-D tensor to vector;
• into_rawvec(): move raw tensor to vector; this does not assume output memory bulk layout is the same to tensor layout.

We do not provide functions that give &[T] or &mut [T]. However, we provide function as_ptr() and as_mut_ptr(), giving the pointer of the first element.

Please note the above mentioned utilities only works in CPU. For other devices (will implemented in future), you may wish to first convert tensor into CPU, then perform Tensor to Vec<T> conversion.

As an example, we compute matrix-vector multiplication and report Vec<f64>:

#![allow(unused)]
fn main() {
    // generate *dynamic* 2-D tensor (vec![3, 4] is dynamic)
    let a = rt::arange(12.0).into_shape(vec![3, 4]);
    let b = rt::arange(4.0);

    // matrix multiplication (gemv 2-D x 1-D case)
    let c = a % b;
    println!("{:?}", c);
    let ptr_1 = c.rawvec().as_ptr();

    // convert to Vec<f64>
    let c = c.into_vec();
    let ptr_2 = c.as_ptr();

    println!("{:?}", c);
    println!("{:?}", core::any::type_name_of_val(&c));
    assert_eq!(c, vec![14.0, 38.0, 62.0]);

    // memory has been moved and no copy occurs if using `into_vec` instead of `to_vec`
    assert_eq!(ptr_1, ptr_2);
}

2.3 Tensor and scalar conversion

RSTSR do not provide method that directly convert T to 0-D tensor Tensor<T, Ix0, B>. For convertion of 0-D tensor Tensor<T, Ix0, B> to T, we provide to_scalar function.

As an example, we compute innerdot and report float result:

#![allow(unused)]
fn main() {
    // a: [0, 1, 2, 3, 4]
    let a = rt::arange(5.0);

    // b: [4, 3, 2, 1, 0]
    let b = rt::arange(5.0);
    let b = b.slice(slice!(None, None, -1)); // or b.flip(0)

    // matrix multiplication (dot product for 1-D case)
    let c = a % b;

    // to now, it is still 0-D tensor
    println!("{:?}", c);

    // convert to scalar
    let c = c.to_scalar();
    println!("{:?}", c);
    assert_eq!(c, 10.0);
}

3. Dimension Conversion

RSTSR provides fixed dimension and dynamic dimension tensors. Dimensions can be converted by into_dim::<D>() or into_dyn.

#![allow(unused)]
fn main() {
    // fixed dimension
    let a = rt::arange(12).into_shape([3, 4]);
    println!("{:?}", a);
    // output: 2-Dim, contiguous: Cc

    // convert to dynamic dimension
    let a = a.into_dim::<IxD>(); // or a.into_dyn();
    println!("{:?}", a);
    // output: 2-Dim (dyn), contiguous: Cc

    // convert to fixed dimension again
    let a = a.into_dim::<Ix2>();
    println!("{:?}", a);
    // output: 2-Dim, contiguous: Cc
}

We only touched array creation with fixed dimension. To create array with dynamic dimension, use Vec<T> instead of [T; N]:

#![allow(unused)]
fn main() {
    let a = rt::arange(12).into_shape(vec![3, 4]);
    println!("{:?}", a);
    // output: 2-Dim (dyn), contiguous: Cc
}

Fixed dimension will be more efficient than dynamic dimension. However, in many arithmetic computations, depneding on contiguous of tensors, the efficiency difference will not be very notable.

Basic Slicing and Indexing

It is a very common usage to extract sub-matrix from matrix, or indexing tensor to lower dimension sub-tensor, to perform future computation.

RSTSR provides most functionality that NumPy calls "basic indexing", which gives tensor view instead of owned tensor. By this mechanism, most tensor extraction operation can be performed without memory copy. For large tensors, cost of all basic slicing and indexing operations are cheap, compared to memory assignment and tensor arithmetics.

Due to language limit, in rust, indexing by brackets [] can only return underlying data &T, so it is not able to return a tensor view by brackets [] technically. In RSTSR, elementwise indexing by [] will return reference of element &T, only if data is stored by Vec<T> type. Usage of [] indexing is quite limited.

However, to obtain sub-tensor view TensorView (or TensorMut) by using function to index and slice is possible. The most important functions and macros to perform slicing are

• slice (equivalntly i): return tensor view by feeding slice parameters;
• slice_mut (equivalntly i): return mutable tensor view by feeding slice parameters;
• slice!((start, ) stop (, slice)): generate slice configuration, which should be similar to python's intrinsic slice function.
• s![]: generate slice parameters (useful when different types of slicing and indexing occurs in the same time); in most scenarios this macro can be substituted by tuple of different types;

Note that we have not implemented advanced indexing. Advanced indexing is mainly about indexing by integer tensor, by boolean tensor, or by index list. These are well covered in numpy, but will be difficult for RSTSR. In most cases, advanced indexing requires (or more efficient when there is) explicitly memory copy. We will persuit to realize some of advanced indexing features in future.

Terminology

• Slicing (by range or slice): $n$-D tensor to $n$-D tensor operation, giving a view of smaller tensor;
• Indexing (by integer): $n$-D tensor to $(n-1)$-D tensor, margining out one dimension by selecting;
• Elementwise Indexing (by list of integer): give reference of element &T instead of giving tensor view.

In RSTSR, slicing and indexing are implemented in a similar way. User can usually simutanously perform slicing and indexing, whenever rust allows.

RSTSR follows rust, C and python convention of 0-based indexing, which is different to Fortran.

1. Indexing by Number

For example, a 3-D tensor $A_{ijk}$ can be indexed into 2-D tensor $B_{jk}=A_{2jk}$:

#![allow(unused)]
fn main() {
    // generate 3-D tensor A_ijk
    let a = rt::arange(24).into_shape([4, 3, 2]);
    println!("{:}", a);

    // B_jk = A_ijk where i = 2
    let b = a.slice(2); // equivalently `a.i(2)`
    println!("{:}", b);
    // output:
    // [[ 12 13]
    //  [ 14 15]
    //  [ 16 17]]
}

Further more, if you wish to perform indexing to both $i=2,j=0$, or say $C_k=A_{20k}$, then you can pass [2, 0] into slice function:

#![allow(unused)]
fn main() {
    // C_k = A_ijk where i = 2, j = 0
    // surely, `a.slice(2).slice(0)` works, but we can use `a.slice([2, 0])` instead
    let c = a.slice([2, 0]);
    println!("{:}", c);
    // output: [ 12 13]
}

RSTSR also accepts negative indices for indexing from the end of the array:

#![allow(unused)]
fn main() {
    // D_jk = A_ijk where i = -1 = 3 (negative index from the end)
    let d = a.slice(-1);
    println!("{:}", d);
    // output:
    // [[ 18 19]
    //  [ 20 21]
    //  [ 22 23]]
}

2. Basic Slicing

2.1 Slicing by range

For example, we want to extract $1\le i<3$ from tensor $A_{ijk}$:

#![allow(unused)]
fn main() {
    // generate 3-D tensor A_ijk
    let a = rt::arange(24).into_shape([4, 3, 2]);
    println!("{:}", a);

    // B_ijk = A_ijk where 1 <= i < 3
    let b = a.slice(1..3); // equivalently `a.i(1..3)`
    println!("{:}", b);
    // output:
    // [[[ 6  7]
    //   [ 8  9]
    //   [10 11]]
    //
    //  [[12 13]
    //   [14 15]
    //   [16 17]]]
}

First two dimensions slicing are also available by the following way:

#![allow(unused)]
fn main() {
    // C_ijk = A_ijk where 1 <= i < 3, 0 <= j < 2
    let c = a.slice([1..3, 0..2]);
    println!("{:}", c);
    // output:
    // [[[ 6  7]
    //   [ 8  9]]
    //
    //  [[12 13]
    //   [14 15]]]
}

Negative indices are also applicable for this case:

#![allow(unused)]
fn main() {
    let a = rt::arange(24);
    // D_i = A_i where i = -5..-2 = 19..22 (negative index from the end given 24 elements)
    let d = a.slice(-5..-2);
    println!("{:}", d);
    // output: [ 19 20 21]
}

2.2 Slicing by ranges

Not only range types (like 1..3) is accepted in RSTSR, but also range to (..3) or range from (1..).

#![allow(unused)]
fn main() {
    let a = rt::arange(24);
    // D_i = A_i where i = -5.. or 19..
    let d = a.slice(-5..);
    println!("{:}", d);
    // output: [ 19 20 21 22 23]
}

But as a remainder, rust does not allow two different types to be merged as rust array [T]:

    // generate 3-D tensor A_ijk
    let a = rt::arange(24).into_shape([4, 3, 2]).into_owned();

    // different types can't be merged into rust array
    // - `..` is RangeFull
    // - `1..3` is Range
    // - `..2` is RangeTo
    let b = a.slice([.., 1..3, ..2]);

To resolve this problem, you may use s! macro, or either just pass tuple (T1, T2) instead of rust array [T]:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);
    let b = a.slice((.., 1..3, ..2)); // equivalently `a.slice(s![.., 1..3, ..2])`
    println!("{:}", b);
    // output:
    // [[[ 2 3]
    //   [ 4 5]]
    //
    //  [[ 8 9]
    //   [ 10 11]]
    //
    //  [[ 14 15]
    //   [ 16 17]]
    //
    //  [[ 20 21]
    //   [ 22 23]]]
}

We just implemented tuple up to 10 elements; if your tensor is extremely high in number of dimensions, you may wish to use s!.

3. Special Indexing

3.1 Slicing with strides

To slice with stride, you may use slice! macro. The usage of slice! macro is similar to python's intrinsic function slice¹:

• slice!(stop): similar to range to ..stop;
• slice!(start, stop): similar to range start..stop;
• slice!(start, stop, step): this is similar to fortran's or numpy's slicing start:stop:step.

#![allow(unused)]
fn main() {
    let a = rt::arange(24);

    // first 5 elements
    let b = a.slice(slice!(5));
    println!("{:}", b);
    // output: [ 0 1 2 3 4]

    // elements from 5 to -9 (resembles 15 for the given 24 elements)
    let b = a.slice(slice!(5, -9));
    println!("{:}", b);
    // output: [ 5 6 7 ... 12 13 14]

    // elements from 5 to -9 with step 2
    let b = a.slice(slice!(5, -9, 2));
    println!("{:}", b);
    // output: [ 5 7 9 11 13]

    // reversed step 2
    let b = a.slice(slice!(-9, 5, -2));
    println!("{:}", b);
    // output: [ 15 13 11 9 7]
}

In many cases, None is also valid input for slice!. In fact, slice! is realized by mechanics of Option<T>, so using Some(val) is also valid.

#![allow(unused)]
fn main() {
    let b = a.slice(slice!(None, 9, Some(2)));
    println!("{:}", b);
    // output: [ 0 2 4 6 8]
}

3.2 Inserting axes

You can insert axes by None or NewAxis (by definition Indexer::Insert). This is similar to numpy's None or np.newaxis.

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    // insert new axis at the beginning
    let b = a.slice(NewAxis);
    println!("{:?}", b.layout());
    // output: shape: [1, 4, 3, 2], stride: [6, 6, 2, 1], offset: 0

    // using `None` is equivalent to `NewAxis`
    let b = a.slice(None);
    println!("{:?}", b.layout());
    // output: shape: [1, 4, 3, 2], stride: [6, 6, 2, 1], offset: 0

    // insert new axis at the second position
    let b = a.slice((.., None));
    println!("{:?}", b.layout());
    // output: shape: [4, 1, 3, 2], stride: [6, 2, 2, 1], offset: 0
}

Using None can be elegent, however, we do not accept Some(val) for indexing. So although the following code compiles, it simply does not work.

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    // insert new axis at the beginning
    let b = a.slice(Some(2));
    println!("{:?}", b.layout());
    // panic: Option<T> should not be used in Indexer.
}

3.3 Ellipsis

In RSTSR, you may use Ellipsis (by definition Indexer::Ellipsis) to skip some indexes:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    // using ellipsis to select index from last dimension
    // equivallently to `a.slice((.., .., 0))` for 3-D tensor
    // same to numpy's `a[..., 0]`
    let b = a.slice((Ellipsis, 0));
    println!("{:2}", b);
    // output:
    // [[  0  2  4]
    //  [  6  8 10]
    //  [ 12 14 16]
    //  [ 18 20 22]]
}

3.4 Mixed indexing and slicing

As mentioned before, using array type [T] is not suitable for representing various kinds of indexing and slicing. However, you may use macro s! or tuple to perform this task².

#![allow(unused)]
fn main() {
    let a: Tensor<f64, _> = rt::zeros([6, 7, 5, 9, 8]);

    // mixed indexing
    let b = a.slice((slice!(-2, 1, -1), None, None, Ellipsis, 1, ..-2));
    println!("{:?}", b.layout());
    // output: shape: [3, 1, 1, 7, 5, 6], stride: [-2520, 360, 360, 360, 72, 1], offset: 10088
}

4. Elementwise Indexing

4.1 Safe elementwise indexing

To perform indexing, you may use rust's bracket []:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    let val = a[[2, 2, 1]];
    println!("{:}", val);
    // output: 17

    println!("{:}", std::any::type_name_of_val(&val));
    // output: i32
}

If you provides index out-of-bound, RSTSR will panic:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    let val = a[[2, 2, 3]];
    println!("{:}", val);
    // panic: Error::ValueOutOfRange : "idx" = 3 not match to pattern 0..(shp as isize) = 0..2
}

It is different in RSTSR in indexing (to tensor view) and elementwise indexing (to reference of value).

#![allow(unused)]
fn main() {
    let view = a.slice((2, 2, 1));
    println!("{:}", view);
    // output: 17

    // it seems to be a value, but actually it is a tensor view
    println!("{:?}", view);
    // output:
    // === Debug Tensor Print ===
    // 17
    // DeviceFaer { base: DeviceCpuRayon { num_threads: 0 } }
    // 0-Dim (dyn), contiguous: CcFf
    // shape: [], stride: [], offset: 17
    // ==========================
}

4.2 Unchecked elementwise indexing

Unchecked elemtwise indexing will be slightly faster than safe elementwise indexing. To perform indexing, you may use unsafe function index_uncheck:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    let val = unsafe { a.index_uncheck([2, 2, 1]) };
    println!("{:}", val);
    // output: 17
}

If you provides index out-of-bound, if the index is still smaller than the underlying memory size, RSTSR will not panic and give wrong value:

#![allow(unused)]
fn main() {
    let a = rt::arange(24).into_shape([4, 3, 2]);

    let val = unsafe { a.index_uncheck([2, 2, 3]) };
    println!("{:}", val);
    // output: 19
    // not desired: last dimension index 3 is out of bound
}

This function is marked unsafe in order to avoid such kind of out-of-bound (but not out-of-memory). In most cases it is still memory safe, in that out-of-memory accessing Vec<T> will gracefully panics.

Arithmetics and Broadcasting

As a tensor toolkit, many basic arithmetics are available in RSTSR.

We will touch arithmetics only in this section, and will mention computations based on mapping in next section.

1. Examples of Arithmetics Operations

RSTSR can handle +, -, *, / operations:

#![allow(unused)]
fn main() {
    let a = rt::arange(5.0);
    let b = rt::arange(5.0) + 1.0;

    let c = &a + &b;
    println!("{:}", c);
    // output: [ 1 3 5 7 9]

    let d = &a / &b;
    println!("{:6.3}", d);
    // output: [ 0.000 0.500 0.667 0.750 0.800]

    let e = 2.0 * &a;
    println!("{:}", e);
    // output: [ 0 2 4 6 8]
}

RSTSR can handle matmul operations by operator % (matrix-matrix, matrix-vector or vector-vector inner dot, and has been optimized in some devices such as DeviceFaer):

#![allow(unused)]
fn main() {
    let mat = rt::arange(12).into_shape([3, 4]);
    let vec = rt::arange(4).into_shape([4]);

    // matrix multiplication
    let res = &mat % mat.t();
    println!("{:3}", res);
    // output:
    // [[  14  38  62]
    //  [  38 126 214]
    //  [  62 214 366]]

    // matrix-vector multiplication
    let res = &mat % &vec;
    println!("{:}", res);
    // output: [ 14 38 62]

    // vector-matrix multiplication
    let res = &vec % &mat.t();
    println!("{:}", res);
    // output: [ 14 38 62]

    // vector inner dot
    let res = &vec % &vec;
    println!("{:}", res);
    // output: 14
}

For some special cases, bit operations and shift are also available:

#![allow(unused)]
fn main() {
    let a = rt::asarray(vec![true, true, false, false]);
    let b = rt::asarray(vec![true, false, true, false]);

    // bitwise xor
    let c = a ^ b;
    println!("{:?}", c);
    // output: [false true true false]

    let a = rt::asarray(vec![9, 7, 5, 3]);
    let b = rt::asarray(vec![5, 6, 7, 8]);

    // shift left
    let c = a << b;
    println!("{:?}", c);
    // output: [ 288 448 640 768]
}

The aforementioned examples should have coverd most usages of tensor arithmetics. The following document in this section will cover some advanced topics.

2. Overrided Operator %

We have already shown that % is the operator for matrix multiplication. This is RSTSR specific usage. This may cause some confusion, and we will discuss this topic.

Firstly, we follow convention of numpy that * will always be elementwise multiply, similar to +, and it does not give matrix multiplication or vector inner dot.

#![allow(unused)]
fn main() {
    let mat = rt::arange(12).into_shape([3, 4]);
    let vec = rt::arange(4);

    // element-wise matrix multiplication
    let c = &mat * &mat;
    println!("{:3}", c);
    // output:
    // [[   0   1   4   9]
    //  [  16  25  36  49]
    //  [  64  81 100 121]]

    // element-wise matrix-vector multiplication (broadcasting involved)
    let d = &mat * &vec;
    println!("{:2}", d);
    // output:
    // [[  0  1  4  9]
    //  [  0  5 12 21]
    //  [  0  9 20 33]]

    // element-wise vector multiplication
    let e = &vec * &vec;
    println!("{:}", e);
    // output: [ 0 1 4 9]
}

Numpy introduces @ notation for matrix multiplication by version 1.10 with PEP 465. For rust, it is virtually hopeless to use the same @ operator as matrix multiplication, which is fully discussed in Rust internal forum (@ has been used as binary operator for pattern binding). To the RSTSR developer's perspective, this is very unfortunate.

Also, other kind of operators (such as %*% for R, .* for Matlab and Julia, . for Mathematica) simply don't exist as binary operator in rust's language. If we wish to that kind of notations, it requires support from programming language level, and this kind of features are not promised to be stablized soon.

However, we consider that though % has been commonly used as remainder, it is less used in vector or matrix computation. % also shares the same operator priority with * and /. Thus, we decided to apply % as matrix multiplication notation if proper.

We reserve name of function rem for remainder computation, and name matmul for matrix multiplication.

#![allow(unused)]
fn main() {
    let a = rt::arange(6);

    // remainder to scalar
    let c = rt::rem(&a, 3);
    println!("{:}", c);
    // output: [ 0 1 2 0 1 2]

    // remainder to array
    let b = rt::asarray(vec![3, 2, 3, 3, 2, 2]);
    let c = rt::rem(&a, &b);
    println!("{:}", c);
    // output: [ 0 1 2 0 0 1]
}

#![allow(unused)]
fn main() {
    let a = rt::arange(6);
    let b = rt::asarray(vec![3, 2, 3, 3, 2, 2]);

    // remainder to array
    let c = rt::rem(&a, &b);
    println!("{:}", c);
    // output: [ 0 1 2 0 0 1]
}

#![allow(unused)]
fn main() {
    // inner product (due to override to `Rem`)
    let c = a.view().rem(&b);
    println!("{:}", c);
    // output: 35
}

3. Broadcasting

Broadcasting makes many tensor operations very simple. RSTSR applies most broadcasting rules from numpy or Python Array API. We refer interested users to numpy and Python Array API documents.

RSTSR initial developer is a computational chemist. We will use an example in chemistry programming, to show how to use broadcasting in real-world situations.

3.1 Example of elementwise multiplication

Sum-of-exponent approximation to RI-MP2 (resolution-identity Moller-Plesset second order perturbation), also termed as LT-OS-MP2, involves the following computation: $${\mathcal{Y}}_{Pia}=Y_{Pia}{ϵ}_i{ϵ}_a$$

#![allow(unused)]
fn main() {
    // task definition
    let (naux, nocc, nvir) = (8, 2, 4); // subscripts (P, i, a)
    let y = rt::arange(naux * nocc * nvir).into_shape([naux, nocc, nvir]);
    let ei = rt::arange(nocc);
    let ea = rt::arange(nvir);
}

This is elementwise multiplication of 3-D tensor with 1-D tensors. In usual cases, the 1-D tensors ${ϵ}_i$ and ${ϵ}_a$ should be expanded and repeated to 3-D counterpart $E_{Pia}^{\mathrm{occ}}={ϵ}_i(\forall P,a)$ and $E_{Pia}^{\mathrm{vir}}={ϵ}_a(\forall P,i)$, then perform multiplication $${\mathcal{Y}}_{Pia}=Y_{Pia}{E}_{Pia}^{\mathrm{occ}}{E}_{Pia}^{\mathrm{vir}}$$ This is both inconvenient and inefficient. By broadcasting, we can insert axis to 1-D tensors, without repeating values: $${\mathcal{Y}}_{Pia}=Y_{Pia}{ϵ}_{\cdot i\cdot }{ϵ}_{\cdot \cdot a}$$

#![allow(unused)]
fn main() {
    // elementwise multiplication with broadcasting
    // `None` means inserting axis, equivalent to `np.newaxis` in NumPy or `NewAxis` in RSTSR
    let converted_y = &y * ei.slice((None, .., None)) * ea.slice((None, None, ..));
}

This multiplication can still be simplified. By numpy's definition of broadcasting rule, it will always add ellipsis at the first dimension. So any operation that inserts axis at the first dimension can be removed: $${\mathcal{Y}}_{Pia}=Y_{Pia}{ϵ}_{i\cdot }{ϵ}_a$$

#![allow(unused)]
fn main() {
    // elementwise multiplication with simplified broadcasting
    let converted_y = &y * &ei.slice((.., None)) * &ea;
}

Finally, for memory and efficiency concern, it is preferred to perform tensor elementwise multiplication of ${ϵ}_{i\cdot }{ϵ}_a$ first: $${\mathcal{Y}}_{Pia}=Y_{Pia}({ϵ}_{i\cdot }{ϵ}_a)$$

#![allow(unused)]
fn main() {
    // optimize for memory access cost
    let converted_y = &y * (&ei.slice((.., None)) * &ea);
}

3.2 Example of matrix multiplication

Many post-HF methods involve integral basis transformation, mostly from raw basis (atomic basis or denoted AO, for example) to molecular orbital basis (denoted MO): $$Y_{Pai}=\sum _{\mu \nu }{Y}_{P\mu \nu }{C}_{\mu i}{C}_{\nu a}$$ This operation involves five indices, $P,\mu ,\nu ,a,i$, where number of indices $a,i$ are smaller than $\mu ,\nu$.

#![allow(unused)]
fn main() {
    // task definition
    let (naux, nocc, nvir, nao, _) = (8, 2, 4, 6, 6); // subscripts (P, i, a, μ, ν)
    let y_ao = rt::arange(naux * nao * nao).into_shape([naux, nao, nao]);
    let c_occ = rt::arange(nao * nocc).into_shape([nao, nocc]);
    let c_vir = rt::arange(nao * nvir).into_shape([nao, nvir]);
}

The broadcasting rule is slightly complicated for matrix multiplication. However, if you are familiar to broadcasting rule, this task can be realized with very simple code:

#![allow(unused)]
fn main() {
    let y_mo = &c_occ.t() % &y_ao % &c_vir;
    println!("{:?}", y_mo.layout());
}

4. Memory Aspects

This is related to how value is passed to arithmetic operations.

4.1 Computation by arithmetic operators

In rust, variable ownership and lifetime rule is strict. The following code will give compiler error:

#![allow(unused)]
fn main() {
    let a = rt::arange(5.0);
    let b = rt::arange(5.0) + 1.0;

    let c = a + b;
    let d = a * b;
}

    |     let c = a + b;
    |                 - value moved here
    |     let d = a * b;
    |                 ^ value used here after move
    |
help: consider cloning the value if the performance cost is acceptable
    |
    |     let c = a + b.clone();
    |                  ++++++++

However, in many cases, performance and memory cost of cloning the tensor is not acceptable. So it is more preferred to perform computation by the following ways, to avoid memory copy and lifetime limitations:

• use reference of tensor,
• use view of tensor,
• use clone of view of tensor,

#![allow(unused)]
fn main() {
    // arithmetic by reference
    let c = &a + &b;

    // arithmetic by view
    let d = a.view() * b.view();

    // view clone is cheap, given tensor is large
    let a_view = a.view();
    let b_view = b.view();
    let e = a_view.clone() * b_view.clone();
}

It should be noted that, except for lifetime limitation, owned tensor is still able to be passed to arithmetic operations. Moreover, inplace arithmetics will be applied when possible (type constraint and broadcastability). For example of 1-D tensor addition, memory of variable c is not allocated, but instead reused from variable a. So if you are sure that a will not be used anymore, you can pass a by value, and that will be more efficient.

#![allow(unused)]
fn main() {
    let a = rt::arange(5.0);
    let b = rt::arange(5.0) + 1.0;
    let ptr_a = a.rawvec().as_ptr();
    // if sure that `a` is not used anymore, pass `a` by value instead of reference
    let c = a + &b;
    let ptr_c = c.rawvec().as_ptr();
    // raw data of `a` is reused in `c`
    // similar to `a += &b; let c = a;`
    assert_eq!(ptr_a, ptr_c);
}

4.2 Computation by associated functions

In RSTSR, there are three ways to perform arithmetic operations:

• by operator: &a + &b;
• by function: rt::add(&a, &b);
• by associated function: (&a).add(&b) or a.view().add(&b).

You may found that code of usage of associated function is somehow weird. In fact, a.add(&b) is also valid in rust, but this will consumes variable a. The following code will not compile due to this problem:

    let a = rt::arange(5.0);
    let b = rt::arange(5.0) + 1.0;

    // below is valid, however `a` is moved
    let c = a.add(&b);

    // below is invalid
    let d = a.div(&b);
    //      ^ value used here after move
    // note: `std::ops::Add::add` takes ownership of the receiver `self`, which moves `a`